Многомассовые расчётные системы.

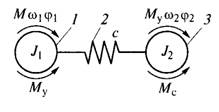1 – первая масса

2 – упругий элемент

3 – вторая масса

Для поступательного движения: C_пр=C_i*S_i²

Для вращательного движения: C_вр=C_к/i_k²

C_i иC_к– коэффициенты жёсткости поступательно движущегося и вращательно движущегося упругого элемента.

Податливостью упругого элемента называют величину обратную жёсткости: е=

Приведение зазоров определятся следующими формулами

При поступательном движении: _пр= ₀*i₀

При вращательном движении: _вр=S₀/ ₀

i₀и ₀– приведённое передаточное число и радиус приведения кинематической цепи.

В данной схеме упругий элемент с коэффициентом жёсткости «С» соединяет две массы с моментами инерции J₁,J₂. Первая из масс включает в себя массу движущейся части двигателя и вращается со скоростью ω₁. В первую массу также входят жёстко связанные с двигателем элементы кинематической схемы.

Вторая масса включает в себя массу ИО РМ и жёстко связанных с ними элементов механической части и вращается со скоростью ω₂. К первой массе приложен момент движения М, момент сопротивления М_с1 и упругий момент М_у. Ко второй массе приложен упругий момент М_уи момент нагрузки М_с2. Уравнение движения двухмассовой системы описывается системой уравнения:

М-М_у-М_с1=J₁*  

М- М_с2=J₂*  

М_с1=C*( ₁- ₂)

₁и ₂– углы поворота первой и второй масс.

Если момент двигателя и момент сопротивления второй массы не изменяется

М=const; M_C2=const 

а момент сопротивления первой массы бесконечно малM_C1 0, то исходное дифференциальное уравнение для скорости первой массы будет иметь вид:

T_y*(d³* ₁/dt³)+d ₁/dt=(M-M_C2)/(J₁+J₂)= _кр

T_y– период свободных колебаний в двухмассовой упругой системе

T_y= (J₁*J₂/C*( J₁+J₂))

_кр– среднее ускорение ЭП.

Используя начальные условия: М_унач=М_С2 и _нач= _2нач=0

скорость первой массы можно определить следующим уравнением:

₁= _ср*t+(T_y* J_{2* ср}/J₁)*sin(t/ T_y)