Метод сканирования.

Метод сканирования заключается в последовательном просмотре значений критерия оптимальности в ряде точек, принадлежащих области изменения независимых переменных, и нахождения среди этих точек такой, в которой критерий оптимальности имеет минимальное (максимальное) значение. Точность метода зависит от того, насколько «густо» располагаются выбранные точки в допустимой области изменения независимых переменных.

Основным достоинством метода сканирования является то, что при его использовании с достаточно «густым» расположением исследуемых точек всегда гарантируется отыскание глобального оптимума, так как анализируется вся область изменения независимых переменных. Другое достоинство – независимость поиска от вида оптимизируемой функции.

         К недостаткам метода относится, в первую очередь, необходимость вычисления значений целевой функции для большого числа точек. Это должно гарантировать, что оптимум не будет пропущен при применении данного метода поиска.

Общий недостаток градиентных методов оптимизации, за исключением, может быть, метода «тяжелого шарика», состоит в том, что все они застревают в ближайшем локальном оптимуме, в область «притяжения» которого попадает выбранная начальная точка спуска. В отличие от этих методов метод сканирования никак не связан наличием локальных оптимумов целевой функции. Поэтому его можно использовать иногда для предварительного грубого установления границ областей «притяжения» указанных оптимумов, после чего могут уже применяться градиентные методы спуска для измерения точной «глубины» каждого локального оптимума.

Наиболее простой алгоритм поиска оптимума методом сканирования, называемый еще иногда сканированием по сетке, заключается в том, что по каждой из независимых переменных даются приращения в соответствующем порядке, обеспечивающем заполнение всей области изменения этих переменных равномерной и достаточно густой сеткой. В простейшем случае двух переменных X₁ и X₂ сканирование сводится к просмотру значений критерия оптимальности при заданном значении одной переменной X₂  для ряда значений другой переменной X₁, которые определяются как отстоящие друг от друга на величину шага Δ X₁ по переменной X_1. После того, как весь диапазон изменения переменной X₁ при заданном значении X₁ исследован и для него найдено минимальное значение критерия оптимальности, изменяется значение переменной X₂ также на величину некоторого шага Δ X₂ по этой переменной и т.д.

Дополнительные ограничения на независимые переменные по существу не усложняют процедуры использования метода сканирования, так как в этом случае точки, которые не удовлетворяют заданным условиям, просто исключаются из рассмотрения и значения критерия оптимальности в них не вычисляются. Наличие дополнительных ограничений на независимые переменные даже ускоряет решение задачи, если, конечно, эти ограничения не заданы в виде трудновычислимых соотношений, поскольку возможный диапазон измерения переменных при этом сужается и значения критерия оптимальности рассчитываются в меньшем числе точек.

Особенно просто обстоит дело, если ограничения заданы в виде неравенств, когда приемлемость точки решается простой проверкой этих условий. Однако метод сканирования можно применить также и в случае, если ограничения имеют вид неравенств.

Таким образом, число вычислений критерия оптимальности при определении положения оптимума методом сканирования возрастает в показательной зависимости от размерности решаемой задачи. Поэтому эффективное применение данного метода в основном ограничивается задачами невысокой размерности n = 2..3, если используется простейший алгоритм поиска, рассмотренный выше, для отыскания оптимума с невысокой точностью.

         Существуют различные модификации метода сканирования, применяемые в основном, для сокращения объема вычислений. Одна из таких модификаций заключается в том, что используется алгоритм с переменным шагом сканирования. Вначале величина шага выбирается достаточно большой, по возможности превышающей требуемую точность определения положения оптимума и выполняется грубый поиск, который локализует область нахождения локального оптимума. После того, как область определена, производится поиск с меньшим шагом только в пределах указанной области. Практически можно организовать целый ряд таких процедур последовательного уточнений положения оптимума. Необходимый объем вычислений значений целевой функции при этом существенно сокращается.

         Важнейшим моментом при использовании метода сканирования с переменным шагом является выбор начального грубого шага поиска. Если начальная величина шага выбрана слишком большой, то может возникнуть опасность пропуска глобального оптимума. Если же начальный шаг выбран слишком малым, то может быть велик необходимый для поиска объем вычислений. При выборе величины начального шага существенную помощь может оказать информация о поведении целевой функции, наличии локальных экстремумов и т.д.

         Имеются и другие модификации метода сканирования, например, сканирование по спирали.

РАСЧЕТНАЯ ЧАСТЬ.

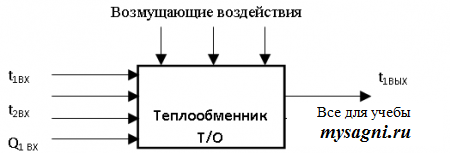
Статическая модель объекта.

Входные параметры:

t_1ВХ- входная температура сырой нефти

t_2ВХ - входная температура готовой нефти

t_1ВЫХ- выходная температура сырой нефти

t_2ВЫХ- выходная температура готовой нефти

Q_{1ВХ –} входной расход сырой нефти

Q_{2ВХ –} входной расход сырой нефти

Q_{1ВХ –} входной расход сырой нефти

Q_{2ВХ –} входной расход сырой нефти

Y – выходная температура готовой нефти       

Необходимо получить зависимость выходной температуры готовой нефти от входных от параметров процесса. В качестве изучаемых факторов, от которых зависит выходной параметр выбираем следующие:

t_1ВХ- входная температура сырой нефти

t_2ВХ - входная температура готовой нефти

Q_{1ВХ –} входной расход сырой нефти

Q_{2ВХ –} входной расход сырой нефти

Исходным статистическим материалом служит выборка объемом в 60 измерений, собранная с изучаемого объекта в режиме нормальной эксплуатации (пассивный эксперимент).