--- / Планирование лекция "Выбор модели. Модель - это вид функции отклика вида"
(автор - student, добавлено - 27-04-2013, 23:05)
Выбор модели. Модель - это вид функции отклика вида
У = Г(Х|,Х2) ....Хц) Вобрать модель - значит выбрать вид этой функции, записать ее уравнение. После этого останется спланировать и провести эксперимент для оценки численных значений ( коэффициентов ) этого уравнения. Геометрическим аналогом функции отклика является поверхность отклика 8. На рис. показана поверхность отклика для случая с двумя факторами. Здесь каждому состоянию " черного ящика." соответствует точка на плоскости Х|ОХ2. \У 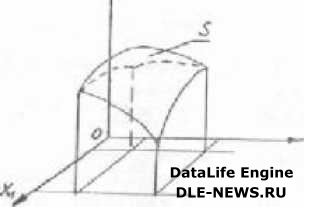 На нижнем рис. пунктирные линии - границы областей определения каждого из факторов, сплошные линии - границы их совместной области определения. А Пространство,в и котором называется факторным пространством. \ 1ри числе факторов больше двух наглядно* ть т 'ряется. Для двух факторов можно даже не переходить к трехмерному пространству, а ограничиться плоскостью (см. рис. ниже), где каждая линия соответствует постоянному значению параметра оптимизации (линия рыного отклика). Каждому вовможному состоянию "черного ящика" соответствует одно значение параметра оптимизации. Однако обратное положение неверно. В дальнейшем стоит задача -остановки эксперимента, чтобы найти оптимум при минимуме затрат. Подойдем к возможности выбора того состояния, которое соответствует наилучшему отклику. Однако это возможно только при наличии таблицы, где содержались бы все возм ожные состояния объекта и соответствующие им отклики. Но этого нет, т.к. при этом нет необходимости построения математической мод ‘ли. Другая возможности - случайный вывод некоторого числа состояний и определение откликов в них, в надежде, что среди них попадутся оптимальные или близкие к нему со стояния. Этот принцип не рационален. Наконец, тре' ья возможность - строить математическую модель, чтобы с ее помощью предсказать значения откликов в тех состояниях, которые не изучались экс периментально. Если не можем измерять отклик в каждом состоянии, то сумеем хотя бы предсказывать результат. Причем только в тех, которые приближают нас к оптимуму. Такой подход приводит к шаговому принципу, лежащему в основе метода планирования эксперимента. 5.1. Шаговой принцип. Априори - предположения относительно свойств неизвестной нам модели до начала эксперимента. Предположения, которые мы не сможем никдгда проверить, называются постулатами. Постулаты, например, это непрерывность поверхности отклика, ее гладкость и наличие единственного оптимума. Они позволяют представить изучаемую функцию в виде степенного ряда в окрестности любой возможной точки факторного пространства. На рисунке показаны: 1. Благоприятный случай. 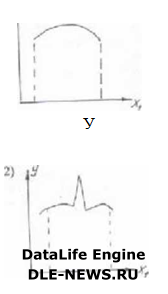 Во втором случае много нарушений: здесь два экстремума (оптимума) и нарушение гладкости (наличие пика). Если мы будем знать значения пар аметра оптимизации в нескольких соседних точках факторного пространства, мы сможем ( в силу гладкости, непрерывности функции отклик^) представить себе результаты, которые можно ожидать в других сосе дних точках. Следовательно, можно найти такие точки, для которых ожидается наибольшее увеличение (или уменьшение) параметра оптимизации. Сделав новый эксперимент, снова можно оценить направление, в котором следу ет скорее всего двигаться. В силу единственности оптимума мы, таким образом, рано или поздно его достигнем. Это и есть шаговый принцип. Некоторые пояснения. Выбирается в факторном пространстве какая-то точка и рассматривается множество точек в ее окрестности, т.е. выбирается малая подобласть. Здесь проводится эксперимент, на основании которого должна быть построена первая модель. Э^а модель используется для предсказания результатов опытов в тех точках, которые не входили в эксперимент. Если эти точки лежат внутри подобласти то предсказание называется интерполяцией, а если вне - экстраполяцией. Чем дальше от области эксперимента лежит точка, тем меньше уверенность предсказания. Поэтому выбирают точку недалеко и используют результаты экстраполяции для выбора условий проведения следующего эксперимента. Дальше цикл повторяется. Ниже на рисунке показаны два способа поиска оптимума, где крестиками обозначены условия опытов. В случае -а) использован классический метод (метод Г аусса-Зейделя) : сначала последовательно изменяется значение одного 11) фактора. Найдя наилучшее значение 1, в этих условиях изменяются значения второго (2) фактора и т.д. (ели факторов - —.. . больше). В случае б) представлен простейший вариант шаговой процедуры: изучается локальная область 1; определив интересующее направление 2, опыты в дальнейшем ставятся в этомАнаправлении. Выбор модели. __ _ о) Главное требование к модели - это способность предсказывать направление дальнейших опытов с требуемой точностью. Это значит, что в 'некоторой подобласти, в которую входят и координаты выполненных опытов, предсказанное с помощью модели значение отклика не должно отличаться от фактического больше, чем на некоторую заранее заданную величину. Модель, удовлетворяющая такому (или аналогичному) требованию, называется адекватой..Проверка выполнимости этого требования называется проверкой адекватности модели. Если окажется несколько адекватных моделей, то выбирают самую простую. 11нже изображена логарифмическая функция. Па некотором оIречке I х, ш „; х 1|1;л ] она с удовлетворительной точностью описывается двумя уравнениями: 1) у = 1оц „ х 2) у = Ьх. В уравнении (2) "в" - коэффициент, который мы можем оценить, например, по результатам эксперимента. В дальнейшем мы будем отдавать предпочтение степенным рядам. Точнее отрезки степенных рядов - алгебраические полиномы. При таком соглашении уравнение (2) проще, чем уравнение (1). Для случая двух факторов полиномы будут: а) полином нулевой степени: у = в 0 ; б) полипом первой степени: у = в п + в,Х| в) полином второй степени: у = в„ + В|\1 В22Х] олиномиачьныемодели. Мы представим неизвестную нам функцию отклика полином. Операция замены одной функции другой, в каком-то смысле эквивалентной функцией называется аппроксимацией. Значит, мы аппроксимировали неизвестную функцию полиномом. При этом нужно найти такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованиям, предъявляемым к модели. Чем ниже степень полинома при значительном числе факторов, тем меньше в нем коэффициентов. г) полином третьей степени: В 222 Х Электронная библиотека АГНИ Нужно, чтобы модель хорошо предсказывала направление наискорейшего улучшения параметра оптимизации. Такое направление называется направлением градиента. Можно ли в этой связи всегда использовать полином первой степени ? Он содержит информацию о направлении градиента, с другой стороны, в нем минимальное число коэффициентов. Вопрос о том, как выбрать подобласть в факторном пространстве, чтобы линейная модель оказалась адекватной. Условие аналитичности функции отклика гарантирует эту возможность. Всегда существует такая окрестность точки (почти любой точки) где линейная модель будет адекватной. Эту размерность окрестности можем находить по результатам опыта. На следующем этапе линейную модель будем искать в следующей (другой) подобласти пока модель перестанет давать эффект. Это значит мы попали в область, близкую к оптимуму, которая называется "почти стационарной". Далее уже нужно опробовать линейную модель ( 1, 2 и т.д. счепени ). Кроме задачи оптимизации, ипо1да ночи икает задача построения интерполяционной модели. Здесь нас не интересует просто оптимум. Мы хотим здесь предсказать результат с требуемой точностью во всех точках некоторой заранее заданной области. Похожие статьи:
|
|
